MI-HGNN: Morphology-Informed Heterogeneous Graph Neural Network for Legged Robot Contact Perception

Daniel Butterfield, Sandilya Sai Garimella, Nai-Jen Cheng, Lu Gan
Georgia Institute of Technology
Submitted to ICRA 2025
Paper Code arXiv
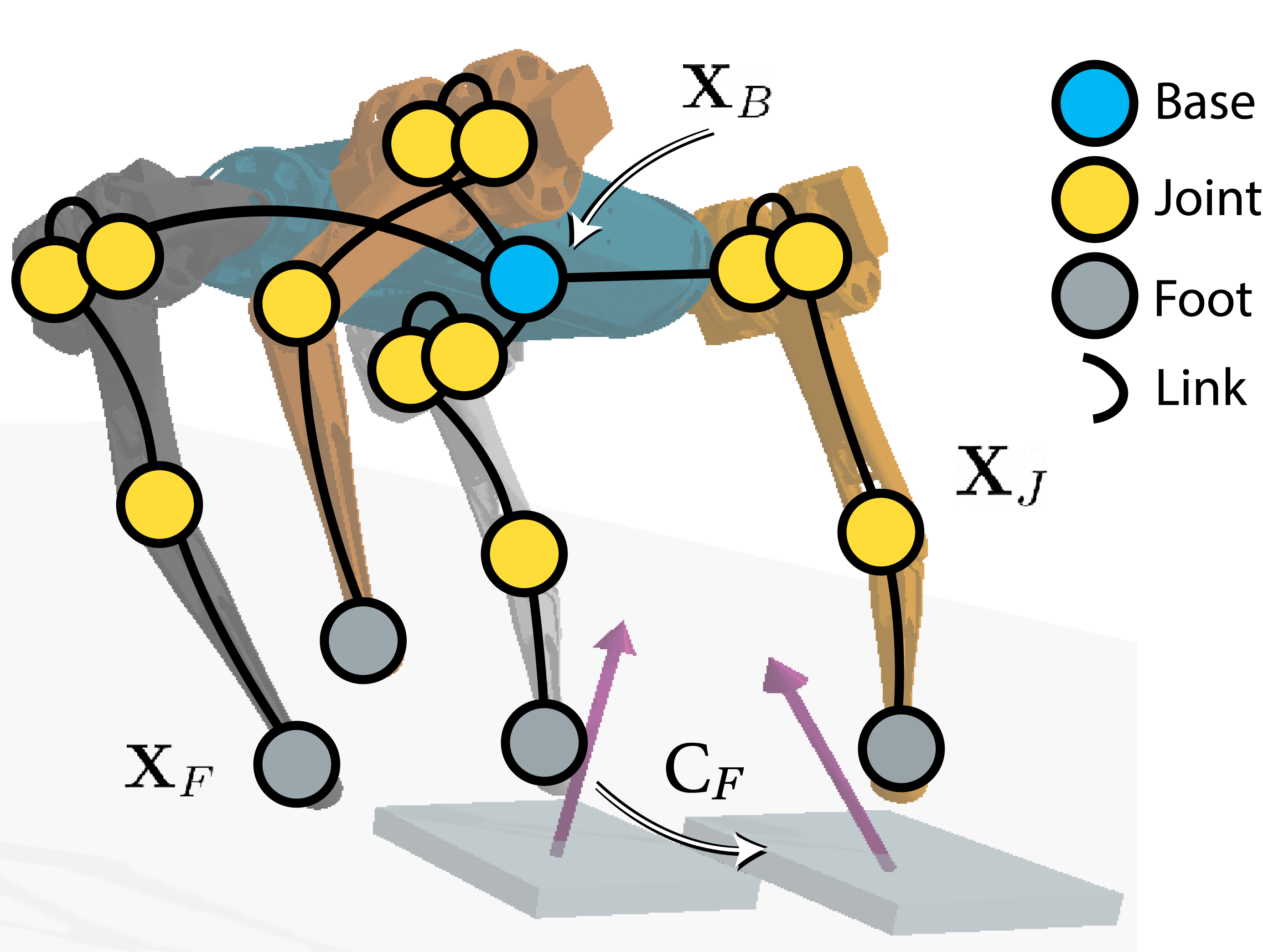
Figure 1; Visualization of our MI-HGNN for the Mini-Cheetah robot as an example.

Abstract

We present a Morphology-Informed Heterogeneous Graph Neural Network (MI-HGNN) for learning-based contact perception. The architecture and connectivity of the MI-HGNN are constructed from the robot morphology, in which nodes and edges are robot joints and links, respectively. By incorporating the morphology-informed constraints into a neural network, we improve a learning-based approach using model-based knowledge. We apply the proposed MI-HGNN to two contact perception problems, and conduct extensive experiments using both real-world and simulated data collected using two quadruped robots. Our experiments demonstrate the superiority of our method in terms of effectiveness, generalization ability, model efficiency, and sample efficiency. Our MI-HGNN improved the performance of a state-of-the-art model that leverages robot morphological symmetry by 8.4% with only 0.21% of its parameters. Although MI-HGNN is applied to contact perception problems for legged robots in this work, it can be seamlessly applied to other types of multi-body dynamical systems and has the potential to improve other robot learning frameworks. Our code is made publicly available at https://github.com/lunarlab-gatech/Morphology-Informed-HGNN.

How does MI-HGNN work?


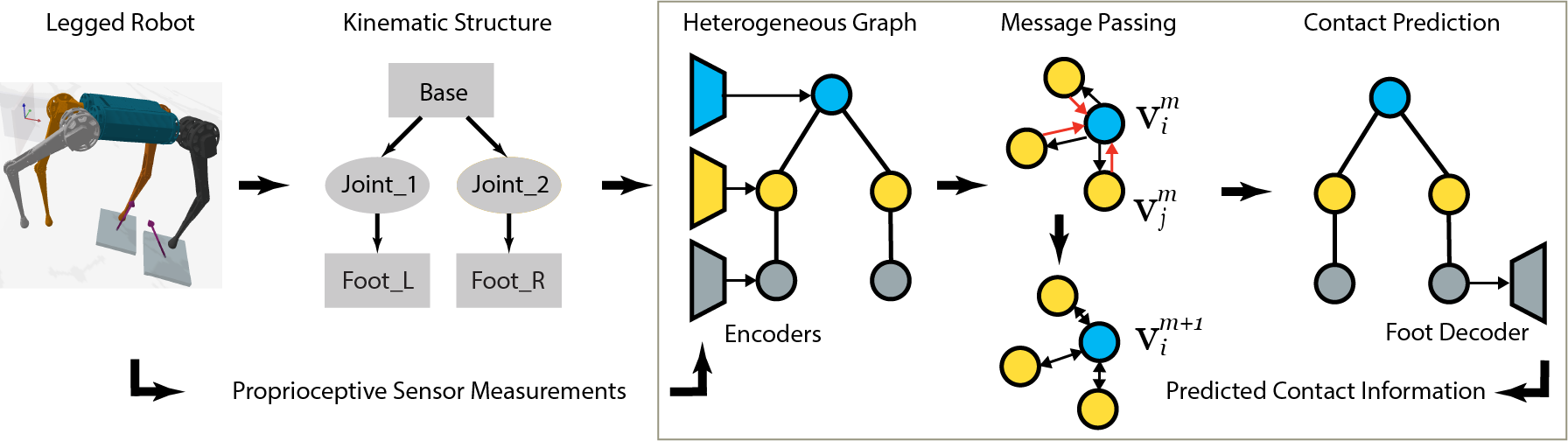
Figure 2; Overview of the proposed MI-HGNN for legged robot contact perception problems.

Our MI-HGNN is constructed from a robot kinematic structure where nodes are joints and edges are links. Proprioceptive sensor measurements acquired at each local frame are embedded into the corresponding node through a heterogeneous encoder, and fused via several layers of message-passing. A foot decoder attached to the foot node exacts the contact information during inference.

Why does MI-HGNN work?


A data correlation aspect: MI-HGNN constrains the learning problem based on the robot's morphology and explicitly captures the correlation and causality between inputs. Message passing between nodes is influenced by intermediate nodes, resembling the physical laws of the robot's system, thereby embedding causality into the message-passing process.

A symmetry aspect: Learned weights are identical between all morphologically-identical limbs of the robotic platform. In addition to reducing the complexity of the search space and lowering model sizes, it allows the model to quickly learn a more generalizable function when compared to completely unconstrained learning models.

What are the benefits of MI-HGNN?

Performance: In terms of contact state accuracy, our MI-HGNN achieves a mean accuracy of 87.7%, improving the performance of the second best ECNN model by 11.3%. Compared with the morphology-agnostic CNN model, our model outperforms it by 22.1%.

Generalization: The real-world and simulated test sets for our experiments incorporate a variety of unseen parameters, including terrains, frictions, and speeds, which demonstrate the generalization ability of the MI-HGNN on out-of-distribution data.

Model Efficiency: Using our smallest MI-HGNN model, we reduce the model parameters from ECNN by a factor of 482 and still improve performance by 8.4%. Therefore, we can achieve performance gains while simultaneously preserving computing resources.

Sample Efficiency: MI-HGNN performance does not drop significantly until the number of training samples is reduced to 10% of the entire training set. In addition, competitive results can still be achieved by our model using only 2.5% of the training set.

Video Presentation

BibTeX

@article{butterfield2024mi,
  title={MI-HGNN: Morphology-Informed Heterogeneous Graph Neural Network for Legged Robot Contact Perception},
  author={Butterfield, Daniel and Garimella, Sandilya Sai and Cheng, Nai-Jen and Gan, Lu},
  journal={arXiv preprint arXiv:2409.11146},
  year={2024},
  eprint={2409.11146},
  url={https://arxiv.org/abs/2409.11146},
}